The experimental data of Vogel & Eaton [1] for air flow and heat transfer in
backward facing step geometry were used to evaluate CFD predictions obtained with the use
of different turbulence models. Specifically we used a Coolit implementation of the eddy
viscosity transport model of Secundov with co-authors [2, 3], several versions of k-e
models [4], and the algebraic model of Deardorff [5]. The k-e models included the standard
and RNG models coupled with the standard and so-called non-equilibrium wall functions [4].
The backward facing step geometry was chosen because it represents a typical building
block of most real-life situations. The step expansion ratio in the experiment was 1.25,
the Reynolds number based on the step height - 28,000, and the wall immediately downstream
of the step had the uniform heat flux 270 W/m2.
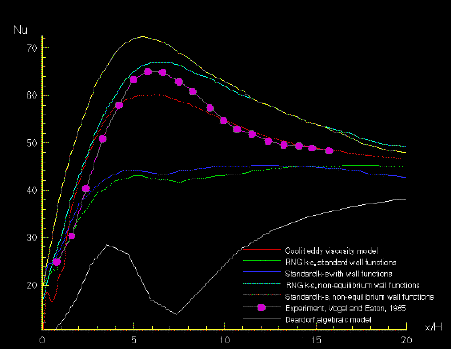
The figure below shows a comparison of computed and measured Nusselt number
distributions along the step side of the experimental section. The superiority of the
Secundov model over both the standard and RNG k-e models with standard wall functions is
clearly seen. The Secundov model also performed tangibly better than the standard k-e
model with non-equilibrium wall functions and was comparable with the RNG-based k-e with
non-equilibrium wall functions. Although the Secundov model somewhat underpredicted the
Nusselt number peak at the re-attachment point, it was considerably more accurate than the
non-equilibrium RNG k-e model in the region of flow recovery after the re-attachment
point.
Considering this fact and important numerical advantages of the Secundov model: it is a
one-equation model, it does not have numerical problems associated with the inflow and
free stream boundary conditions typical for k-e models, it requires a coarser near-wall
grid to get a grid-independent solution (in the law of the wall units the near wall
distance, y+, might be as high as 1.0-1.5 vs. 0.1 typical for low Re versions of k-e
models), leads us to conclude that the Secundov model provides the best combination of
accuracy and computational efficiency for real-life heat transfer problems compared to
existing k-e models. Algebraic subgrid models and similar mixing length models performed
much worse than either of the above and are suitable primarily for qualitative coarse grid
computations.
1. Vogel, J.C, and Eaton, J.K., "Combined Heat Transfer and Fluid Dynamic
Measurements Downstream of a Backward-Facing Step", Transactions of the ASME, Journal
of Heat Transfer, Vol. 107, November 1985, pp. 922-929.
3. Gulyaev, A.N., Kozlov, V.Y.,and Secundov, A.N., "A Universal One-Equation Model
for Turbulent Viscosity," Fluid Dynamics, Vol. 28, No.4, 1993, pp.485-494. See also:
Shur M., Strelets M., Zaikov L., Gulyaev A., Kozlov V., and Secundov A., "Comparative
Numerical Testing of One- and Two-Equation Turbulence Models for Flows with Separation and
Reattachment", AIAA Paper 95-0863, Jan. 1995.
3. Coolit User's Manual, Daat Research Corp., 1997.
4. Fluent Inc. WWW newsletter, http://www.fluent.com/news/Summer95/HeatTran.htm
5. Deardorff J.W., J. Comput. Physics, V.7, 1971, pp.120-133.